Don't forget to +1, Like the videos, and share on Facebook
Questions and comments are welcome!
1. A wheel has a radius of 3.6 m. How far (path length) does a point on the circumference travel if the wheel is rotated through the following angles, respectively
a) 31 °
_____ m
b) 31 rad
_____m
c) 31 rev
_____m
2. The tires on a new compact car have a diameter of 2.0 ft and are warranted for 64,000 miles.
a) Determine the angle (in radians) through which one of these tires will rotate during the warranty period
_________ rad
b) How many revolutions of the tire are equivalent to your answer in (a)?
________ rev
3. A potter's wheel moves uniformly from rest to an angular speed of 0.19 rev/s in 29.0 s.
a) Find its angular acceleration in radians per second per second
________ rad/s2
4. A race car starts from rest on a circular track of radius 433 m. The car's speed increases at the constant rate of 0.320 m/s2 . At the point where the magnitudes of the centripital and tangential accelerations are equal, find the following.
a) the speed of the race car
________m/s
b) the distance traveled
______ m
c) The elapsed time
______ s
5. A dentist drill starts from rest. After 3.30 s of constant angular acceleration it turns at a rate of 2.9 X 104 rev/min.
a) Find the drill's angular acceleration
______ rad/s2
b) Determine the angle (in radians) through which the drill rotates during this period
_________ rad
6. A 53.4-cm diameter disk rotates with a constant angular acceleration of 2.60 rad/s2. It starts from rest at t = 0, and a line drawn from the center of the disk to point p on the rim of the disk makes an angle of 57.3° with the positive x-axis at this time.
a) Find the angular speed of the wheel at t = 2.30 s
______ rad/s
b) Find the linear velocity and tangential acceleration of p at t = 2.30 s.
linear velocity _______ m/s
tangential acceleration _____ m/s2
c) Find the position of P (in degrees, with respect to the positive x-axis) at t = 2.30 s
________ °
7. A rotating wheel requires 6.00 s to rotate 25.0 revolutions. Its angular velocity at the end of the 6.00-s interval is 96.0 rad/s. What is the constant angular acceleration (in rad/s2/) of the wheel
______ rad/s2/
8. A car initially traveling eastward turns north by traveling in a circular path at uniform speed as in the figure. The length of the arc ABC is 249 m, and the car completes the turn in 33.0 s
a) Determine the car's speed
_______ m/s
b) What is the magnitude and direction of the acceleration when the car is at point B?
magnitude _________ m/s2
direction _________ ° counterclockwise from the +x-axis
9. It has been suggested that rotating cylinders about 11 mi long and 3.6 mi in diameter be placed in space and used as colonies. What angular speed must the cylinder have so that the centripetal acceleration at its ssurface equals the free-fall acceleration on Earth?
__________ rad/s
10. An adventurous archeologist (m = 80.5 kg) tries to cross a river by swinging from a vine. The vine is 11.0 m long, and his speed at the bottom of the swing is 8.5 m/s. The archeologist doesn't know that the vine has a breaking strength of 1,000 N. Does he make it safely across he river without falling in?
Yes
No
11. A 55.0-kg ice skater is moving at 4.03 m/s when she grabed the loose end of a rope, the opposite end of which is tied to a pole. She then moves in a circle of radius 0.805 m around the pole
a) Determine the force exerted by the horizontal rope on her arms.
_______N
b) Compare this force with her weight by finding the ratio of the force to her weight
_________
12. A certain light truck can go around a flat curve having a radius of 150 m with a maximum speed of 30.5 m/s. With what maximum speed can it go around a curve having a radius of 85.5 m?
_________m/s
13. A 50.0-kg child stands at the rim of a merry-go-round of radius 2.10 m, rotating with an angular speed of 2.6 rad/s
a) What is the child's centripetal acceleration?
________ m/s2
b) What is the minimum force between her feet and the floor of the carousel that is required to keep her in the circular path?
________N
c) What minimum coefficient of static friction is required?
__________
Is the answer you found reasonable? In other words, is she likely to stay on the merry-go-round?
Yes
No
14. An air puck of mass m1 = 0.30 kg is tied to a string and allowed to revolve in a circle of radius R = 1.3 m on a frictionless horizontal table. The other end of the string passes through a hole in the center of the table, and a mass of m2 = 1.1 kg is tied to it (see the figure below). The suspended mass remains in equilibrium while the puck on the tabletop revolves.
a) What is the tension in the string?
_______ N
b) What is the horizontal force acting on the puck?
_______N
c) What is the speed of the puck?
_______m/s
15. The average distance separating Earth and the moon (center to center) is 384,000 km. Use the data in the table to find the net gravitational force exerted by the Earth and the Moon on a 3.00 x 104-kg spaceship located halfway between them.
________ N
16. A satelite has a mass of 99 kg and is located at 2.05 x 106 m above the surface of the Earth.
a) What is the potential energy associated with the satelite at this location?
________ J
b) What is the magnitude of the gravitational force on the satelite?
_______ N
17. A coordinate system (in meters) is constructed on the surface of a pool table, and three objects are placed on the table as follows: a 7.0-kg object at the origin of the coordinate system, a 16.0-kg object at (0, 2.0), and a 25.0-kg object at (4.0, 0). Find the resultant gravitational force exerted by the other two objects on the object at the origin.
Magnitude _________ N
direction ________°
18. Objects with masses of 190 kg and a 490 kg are separated by 0.430 m.
a) Find the net gravitational force exerted by these objects on a 65.0-kg object placed midway between them.
magnitude _______ N
direction
- Toward the 190-kg mass
- Toward the 490-kg mass
- The magnitude is zero
19. A satelite is in a circular orbit around the Earth at an altitude of 2.52 x 106 m.
a) find the period of the orbit. (Hint: Modify Kepler's third law:
T2 =
r3
so it is suitable for objects orbiting the Earth rather than the Sun. The radius of the Earth is 6.38 x 106 m, and the mass of the Earth is 5.98 x 1024 kg.)
__________ h
b) Find the speed of the satellite
_______km/s
c) Find the acceleration of the satelite.
_______ m/s2 toward the center of the earth
20. A satellite of Mars, called Phobos, has an orbital radius of 9.4 x 106 m and a period of 2.8 x 104 s. Assuming the orbit is circular, determine the mass of Mars
___________ kg
21. A 549-kg satellite is in a circular orbit about the Earth at a height above the Earth equal to the Earth's mean radius.
a) Find the satellite's orbital speed
_________m/s
b) Find the period of its revolution.
________ h
c) Find the gravitational force acting on it.
_________ N
Questions and comments are welcome!
1. A wheel has a radius of 3.6 m. How far (path length) does a point on the circumference travel if the wheel is rotated through the following angles, respectively
a) 31 °
_____ m
b) 31 rad
_____m
c) 31 rev
_____m
2. The tires on a new compact car have a diameter of 2.0 ft and are warranted for 64,000 miles.
a) Determine the angle (in radians) through which one of these tires will rotate during the warranty period
_________ rad
b) How many revolutions of the tire are equivalent to your answer in (a)?
________ rev
3. A potter's wheel moves uniformly from rest to an angular speed of 0.19 rev/s in 29.0 s.
a) Find its angular acceleration in radians per second per second
________ rad/s2
4. A race car starts from rest on a circular track of radius 433 m. The car's speed increases at the constant rate of 0.320 m/s2 . At the point where the magnitudes of the centripital and tangential accelerations are equal, find the following.
a) the speed of the race car
________m/s
b) the distance traveled
______ m
c) The elapsed time
______ s
5. A dentist drill starts from rest. After 3.30 s of constant angular acceleration it turns at a rate of 2.9 X 104 rev/min.
a) Find the drill's angular acceleration
______ rad/s2
b) Determine the angle (in radians) through which the drill rotates during this period
_________ rad
6. A 53.4-cm diameter disk rotates with a constant angular acceleration of 2.60 rad/s2. It starts from rest at t = 0, and a line drawn from the center of the disk to point p on the rim of the disk makes an angle of 57.3° with the positive x-axis at this time.
a) Find the angular speed of the wheel at t = 2.30 s
______ rad/s
b) Find the linear velocity and tangential acceleration of p at t = 2.30 s.
linear velocity _______ m/s
tangential acceleration _____ m/s2
c) Find the position of P (in degrees, with respect to the positive x-axis) at t = 2.30 s
________ °
7. A rotating wheel requires 6.00 s to rotate 25.0 revolutions. Its angular velocity at the end of the 6.00-s interval is 96.0 rad/s. What is the constant angular acceleration (in rad/s2/) of the wheel
______ rad/s2/
8. A car initially traveling eastward turns north by traveling in a circular path at uniform speed as in the figure. The length of the arc ABC is 249 m, and the car completes the turn in 33.0 s
a) Determine the car's speed
_______ m/s
b) What is the magnitude and direction of the acceleration when the car is at point B?
magnitude _________ m/s2
direction _________ ° counterclockwise from the +x-axis
9. It has been suggested that rotating cylinders about 11 mi long and 3.6 mi in diameter be placed in space and used as colonies. What angular speed must the cylinder have so that the centripetal acceleration at its ssurface equals the free-fall acceleration on Earth?
__________ rad/s
10. An adventurous archeologist (m = 80.5 kg) tries to cross a river by swinging from a vine. The vine is 11.0 m long, and his speed at the bottom of the swing is 8.5 m/s. The archeologist doesn't know that the vine has a breaking strength of 1,000 N. Does he make it safely across he river without falling in?
Yes
No
11. A 55.0-kg ice skater is moving at 4.03 m/s when she grabed the loose end of a rope, the opposite end of which is tied to a pole. She then moves in a circle of radius 0.805 m around the pole
a) Determine the force exerted by the horizontal rope on her arms.
_______N
b) Compare this force with her weight by finding the ratio of the force to her weight
_________
12. A certain light truck can go around a flat curve having a radius of 150 m with a maximum speed of 30.5 m/s. With what maximum speed can it go around a curve having a radius of 85.5 m?
_________m/s
13. A 50.0-kg child stands at the rim of a merry-go-round of radius 2.10 m, rotating with an angular speed of 2.6 rad/s
a) What is the child's centripetal acceleration?
________ m/s2
b) What is the minimum force between her feet and the floor of the carousel that is required to keep her in the circular path?
________N
c) What minimum coefficient of static friction is required?
__________
Is the answer you found reasonable? In other words, is she likely to stay on the merry-go-round?
Yes
No
14. An air puck of mass m1 = 0.30 kg is tied to a string and allowed to revolve in a circle of radius R = 1.3 m on a frictionless horizontal table. The other end of the string passes through a hole in the center of the table, and a mass of m2 = 1.1 kg is tied to it (see the figure below). The suspended mass remains in equilibrium while the puck on the tabletop revolves.
a) What is the tension in the string?
_______ N
b) What is the horizontal force acting on the puck?
_______N
c) What is the speed of the puck?
_______m/s
15. The average distance separating Earth and the moon (center to center) is 384,000 km. Use the data in the table to find the net gravitational force exerted by the Earth and the Moon on a 3.00 x 104-kg spaceship located halfway between them.
________ N
Useful Planetary Data
|
||||||
Body
|
Mass (kg)
|
Mean Radius (m)
|
Period (s)
|
Distance from Sun (m)
|
T2/r3 (s2/m3)
|
|
Mercury
|
3.18 x 1023
|
2.43 x 106
|
7.60 x 106
|
5.79 x 1010
|
2.97 x 10−19
|
|
Venus
|
4.88 x 1024
|
6.06 x 106
|
1.94 x 107
|
1.08 x 1011
|
2.99 x 10−19
|
|
Earth
|
5.98 x 1024
|
6.37 x 106
|
3.156 x 107
|
1.496 x 1011
|
2.97 x 10−19
|
|
Mars
|
6.42 x 1023
|
3.37 x 106
|
5.94 x 107
|
2.28 x 1011
|
2.98 x 10−19
|
|
Jupiter
|
1.90 x 1027
|
6.99 x 107
|
3.74 x 108
|
7.78 x 1011
|
2.97 x 10−19
|
|
Saturn
|
5.68 x 1026
|
5.85 x 107
|
9.35 x 108
|
1.43 x 1012
|
2.99 x 10−19
|
|
Uranus
|
8.68 x 1025
|
2.33 x 107
|
2.64 x 109
|
2.87 x 1012
|
2.95 x 10−19
|
|
Neptune
|
1.03 x 1026
|
2.21 x 107
|
5.22 x 109
|
4.50 x 1012
|
2.99 x 10−19
|
|
Pluto
|
~1.4 x 1022
|
~1.5 x 106
|
7.82 x 109
|
5.91 x 1012
|
2.96 x 10−19
|
|
Moon
|
7.36 x 1022
|
1.74 x 106
|
-
|
-
|
-
|
|
Sun
|
1.991 x 1030
|
6.96 x 108
|
-
|
-
|
-
|
|
16. A satelite has a mass of 99 kg and is located at 2.05 x 106 m above the surface of the Earth.
a) What is the potential energy associated with the satelite at this location?
________ J
b) What is the magnitude of the gravitational force on the satelite?
_______ N
17. A coordinate system (in meters) is constructed on the surface of a pool table, and three objects are placed on the table as follows: a 7.0-kg object at the origin of the coordinate system, a 16.0-kg object at (0, 2.0), and a 25.0-kg object at (4.0, 0). Find the resultant gravitational force exerted by the other two objects on the object at the origin.
Magnitude _________ N
direction ________°
18. Objects with masses of 190 kg and a 490 kg are separated by 0.430 m.
a) Find the net gravitational force exerted by these objects on a 65.0-kg object placed midway between them.
magnitude _______ N
direction
- Toward the 190-kg mass
- Toward the 490-kg mass
- The magnitude is zero
19. A satelite is in a circular orbit around the Earth at an altitude of 2.52 x 106 m.
a) find the period of the orbit. (Hint: Modify Kepler's third law:
T2 =
 |
| 4π2 |
| GMS |
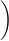 |
so it is suitable for objects orbiting the Earth rather than the Sun. The radius of the Earth is 6.38 x 106 m, and the mass of the Earth is 5.98 x 1024 kg.)
__________ h
b) Find the speed of the satellite
_______km/s
c) Find the acceleration of the satelite.
_______ m/s2 toward the center of the earth
20. A satellite of Mars, called Phobos, has an orbital radius of 9.4 x 106 m and a period of 2.8 x 104 s. Assuming the orbit is circular, determine the mass of Mars
___________ kg
21. A 549-kg satellite is in a circular orbit about the Earth at a height above the Earth equal to the Earth's mean radius.
a) Find the satellite's orbital speed
_________m/s
b) Find the period of its revolution.
________ h
c) Find the gravitational force acting on it.
_________ N


Thanks, Mike! This has been very helpful and I appreciate the time and energy you devote to this blog. What time do you think you will be finished answering the last few questions?
ReplyDeleteAre you going to have time to finish the last 5 questions? I can't seem to figure them out.
ReplyDeleteI agree with the other person that your videos are very helpful! Wouldn't be able to do it without you!
I've been out of town all day. I'm about to post the last five as fast as I possibly can. Sorry for the delay!
ReplyDeleteTotally confused on #18 how you got 689021.0925/6.673x10^11 to equal 4.5978x10^-5. I keep getting 1.033x10^-6
ReplyDeleteI see the mistake I made in the presentation. I actually plugged it in correctly in the calculator, but wrote the expression incorrectly in the video.
DeleteThe form: 6.673 x 10^-11 (689021.0925)
= 6.673 x (689021.0925/10^11)
= )(6.673 X 689021.0925)/(10^11)
= 4.5978 x 10^-5
The mistaken format was to place the 6.673 in the denominator of the fraction.
I'll update the video soon. Thanks for the catch!
In symbolic language:
DeleteA x B^(-n) = A/B^n
In our case 6.673 x 10^-11 = 6.673/10^11
Hope that makes more sense! I was trying to save space on the screen and I messed up the algebra.
Thanks! You're the best. Ugh, I've been frustratingly looking for help online for hours. Thanks so much! Keep posting videos
ReplyDeleteI'm glad you found my blog. Make sure you share with friends!
DeleteYou are such a very helpful man may God richly bless you and your family
ReplyDelete